目的
このコンテンツは,「2つの平面が垂直である」ことの定義を天下り的に与えるのではなく,既に持っている直観的なイメージを基にして,その定義を生徒が自ら作り出していくことを意図したものです。
対象学年及び時期
中学一年生 時期:空間における直線や平面の位置関係
構成
内積を用いて図形の方程式を求める課題として、円錐面の方程式を求める課題を扱います。具体的には、次のような手順で進みます。
① 条件と課題の提示。
② 3次元動的幾何ソフト Cabri3Dの画面で、条件を満たす点Pの様子を操作・観察する。
③ 2つのベクトルの関係から常に成り立つ関係、保存される数量を見出す。
④ 円錐面の方程式の求め方を考える。
⑤ 解説の提示
⑥ 円錐曲線の復習と円錐曲線の方程式を求める問題の提示
⑦ 解説
⑧ 他の切断により得られる双曲線や楕円の方程式を求める問題の提示
生徒が空間図形上のベクトルや点の動きに対する理解が深まるように、段階的に異なるCabri3D画面を配置しています。
スライドの使い方
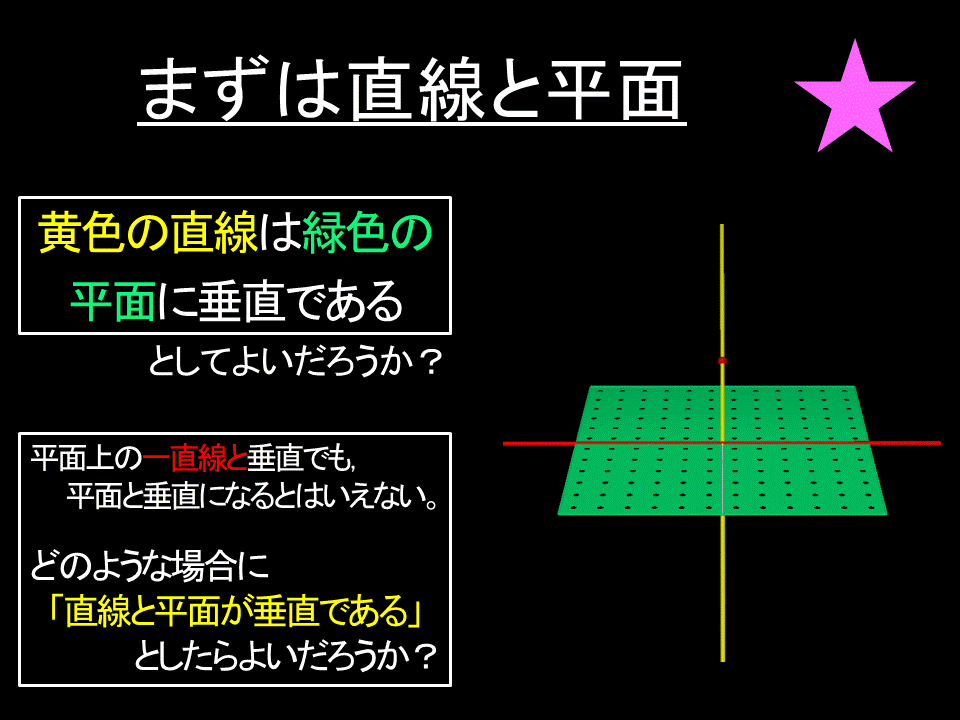
これは,「二平面の垂直」の前に,「直線と平面の垂直」について考えるスライドです。
 |
① まず「右図において黄色の直線は緑色の平面に垂直であるとしてよいだろうか」と
生徒に問いかけます。
② 次に,図を右クリックしながら動かすと,視点を変えることができます。
それによって,「平面上の一直線(赤線)と垂直でも,平面と垂直になるとはいえない」と
いうことを見出すことができます。また,赤色の点を左クリックしながら動かすと,黄色の
直線を動かすこともできます。
③ 図以外の場所でクリックすると左下のテキストボックスが挿入されますので,この
問題について教室で考えてみてください。
④ その後,必要に応じて定義を導入してください。また,三角定規を使った次の問題を
取り上げることも考えられます。
※もしもお使いのコンピュータにCabri 3Dがインストールされていれば,★をクリックすると,
スライドの図形ファイルを開くことができ,より大きな画面で空間図形を操作することができます。